Table of Contents
The library is intended to be both fast and clear for development and research. At the same time, it allows great level of customization and guarantees a high level of accuracy and numerical robustness.
Running your own problems.
The best way to design your own problem is by following one of the examples. Basically, there are 3 steps that should be followed:
- Define the function to optimize.
- Modify the parameters of the optimization process. In general, many problems can be solved with the default set of parameters, but some of them will require some tuning.
- The set of parameters and the default set can be found in parameters.h.
- In general most users will need to modify only the parameters described in Basic parameter setup.
- Advanced users should read Understanding the parameters for a full description of the parameters.
- Set and run the corresponding optimizer (continuous, discrete, categorical, etc.). In this step, the corresponding restriction should be defined.
- Continuous optimization requires box constraints (upper and lower bounds).
- Discrete optimization requires the set of discrete values.
- Categorical optimization requires the number of categories per dimension.
Basic parameter setup
Many users will only need to change the following parameters. Advanced users should read Understanding the parameters for a full description of the parameters.
- n_iterations: Number of iterations of BayesOpt. Each iteration corresponds with a target function evaluation. Curently, this is the only stopping criteria. In general, more evaluations result in higher precision [Default 190]
- noise: Observation noise/signal ratio. [Default 1e-6]
- For stochastic functions (if several evaluations of the same point produce different results) it should match as close as possible the variance of the noise with respect to the variance of the signal. Too much noise results in slow convergence while not enough noise might result in not converging at all.
- For simulations and deterministic functions, it should be close to 0. However, to avoid numerical instability due to model inaccuracies, make it always greater than 0. For example, between 1e-10 and 1e-14.
If execution time is not an issue, accuracy might be improving modifying the following parameters.
- l_type: Learning method for the kernel hyperparameters. Setting this parameter to L_MCMC uses a more robust learning method which might result in better accuracy, but the overall execution time will increase. [Default L_EMPIRICAL]
- n_iter_relearn: Number of iterations between re-learning kernel parameters. That is, kernel learning ocur 1 out of n_iter_relearn iterations. Ideally, the best precision is obtained when the kernel parameters are learned every iteration (n_iter_relearn=1). However, this learning part is computationally expensive and implies a higher cost per iteration. If n_iter_relearn=0, then there is no relearning. [Default 50]
- n_inner_iterations: (only for continuous optimization) Maximum number of iterations (per dimension!) to optimize the acquisition function (criteria). That is, each iteration corresponds with a criterion evaluation. If the original problem is high dimensional or the result is needed with high precision, we might need to increase this value. [Default 500]
API description
Here we show a brief summary of the different ways to use the library. Basically, there are two ways to use the library based on your coding style:
-Callback: The user sends a function pointer or handler to the optimizer, following a prototype. This method is available for C/C++, Python, Matlab and Octave.
-Inheritance: This is a more object oriented method and allows more flexibility. The user creates a module with his function, process, etc. This module inherits one of BayesOpt models, depending if the optimization is discrete or continuous, and overrides the evaluateSample method. This method is available only for C++ and Python.
C usage
This interface is the most standard approach. Due to the large compatibility with C code with other languages it could also be used for other languages such as Fortran, Ada, etc.
The function to optimize must agree with the template provided in bayesopt.h
Note that the gradient has been included for future compatibility, although in the current implementation, it is not used. You can just ignore it or send a NULL pointer.
The parameters are defined in the bopt_params struct. The easiest way to set the parameters is to use
and then, modify the necessary fields. For the non-numeric parameters, there are a set of functions that can help to set the corresponding parameters:
Basically, it just need a pointer to the parameters and a string for the parameter value. For example:
Once we have set the parameters and the function, we can called the optimizer according to our problem.
-For the continuous case:
-For the discrete case:
-For the categorical case:
This interface catches all the expected exceptions and returns error codes for C compatibility.
C++ usage
Besides being able to use the library with the C usage from C++, we can also take advantage of the object oriented properties of the language.
This is the most straightforward and complete method to use the library. The object that must be optimized must inherit from one of the models defined in bayesopt.hpp.
Then, we just need to override the virtual functions called evaluateSample which correspond to the function to be optimized.
Optionally, we can redefine checkReachability to declare nonlinear constrain (if a point is invalid, checkReachability should return false and if it is valid, true). Note that the latter feature is experimental. There is no convergence guarantees if used.
For example, with for a continuous problem, we will define our optimizer as:
where input_dimension is an size_t value with the number of input dimensions of the problem. Note that for C++ we use the Parameters class defined in parameters.hpp for convenience.
Then, we use it like:
For discrete a categorical cases, we just need to inherit from the DiscreteModel. Depending on the type of input we can use the corresponding constructor. In this case, the setBoundingBox step should be skipped.
Optionally, we can also choose to run every iteration independently. See bayesopt.hpp and bayesoptbase.hpp
Python usage
The file python/demo_quad.py provides simple example of different ways to use the library from Python.
- Parameters: The parameters are defined as a Python dictionary with the same structure and names as the Parameters class in the C++ interface, with the exception of kernel.* and mean.* which are replaced by kernel_ and mean_ respectively.
There is no need to fill all the parameters. If any of the parameter is not included in the dictionary, the default value is included instead.
- a) Callback: The callback interface is just a wrapper of the C interface. In this case, the callback function should have the prototype where query is a numpy array and the function returns a double scalar.def my_function (query):
The optimization process for a continuous model can be called as
where the result is a tuple with the minimum as a numpy array (x_out), the value of the function at the minimum (y_out) and an error code.
Analogously, the function for a discrete model is:
where x_set is an array of arrays with the valid inputs.
And for the categorical case:
where categories is an integer array with the number of categories per dimension.
- b) Inheritance: The object oriented methodology is similar to the C++ interface.
Then, the optimization process can be called as
where the result is a tuple with the minimum as a numpy array (x_out), the value of the function at the minimum (y_out) and an error code.
For discrete a categorical cases, we just need to inherit from the bayesoptmodule.BayesOptDiscrete or bayesoptmodule.BayesOptCategorical. See bayesoptmodule.py. In this case, the "set bounds" step should be skipped.
Note: For some "expected" error codes, a corresponding Python exception is raised. However, this exception is raised once the error code is found the Python environment, so it does not have track of any exception happening in the C++ part of the code.
Matlab/Octave usage
The file matlab/runtest.m provides an example of different ways to use BayesOpt from Matlab/Octave.
The parameters are defined as a Matlab struct with the same structure and names as the bopt_params struct in the C/C++ interface, with the exception of kernel.* and mean.* which are replaced by kernel_ and mean_ respectively. Also, C arrays are replaced with vector, thus there is no need to set the number of elements as a separate entry.
There is no need to fill all the parameters. If any of the parameter is not included in the Matlab struct, the default value is automatically included instead.
The Matlab/Octave interface is just a wrapper of the C interface. In this case, the callback function should have the form
where query is a Matlab vector and the function returns a scalar value.
The optimization process can be run for continuous variables (both in Matlab and Octave) as
where the result is the minimum as a vector (x_out) and the value of the function at the minimum (y_out). Analogously, the optimization process for discrete variables:
and for categorical variables:
In Matlab, but not in Octave, the optimization can also be called with function handlers. For example:
Understanding the parameters
BayesOpt relies on a complex and highly configurable mathematical model. In theory, it should work reasonably well for many problems in its default configuration. However, Bayesian optimization shines when we can include as much knowledge as possible about the target function or about the problem. Or, if the knowledge is not available, keep the model as general as possible (to avoid bias). In this part, knowledge about Gaussian processes or nonparametric models in general might be useful.
It is recommendable to read the page about Bayesian optimization in advance.
The parameters are bundled in a structure (C/C++/Matlab/Octave) or dictionary (Python), depending on the API that we use. This is a brief explanation of every parameter.
Budget parameters
This set of parameters have to deal with the number of evaluations or iterations for each step.
- n_iterations: Number of iterations of BayesOpt. Each iteration corresponds with a target function evaluation. In general, more evaluations result in higher precision [Default 190]
- n_iter_relearn: Number of iterations between re-learning kernel parameters. That is, kernel learning ocur 1 out of n_iter_relearn iterations. Ideally, the best precision is obtained when the kernel parameters are learned every iteration (n_iter_relearn=1). However, this learning part is computationally expensive and implies a higher cost per iteration. If n_iter_relearn=0, then there is no relearning. [Default 50]
- n_inner_iterations: (only for continuous optimization) Maximum number of iterations (per dimension!) to optimize the acquisition function (criteria). That is, each iteration corresponds with a criterion evaluation. If the original problem is high dimensional or the result is needed with high precision, we might need to increase this value. [Default 500]
Initialization parameters
Sometimes, BayesOpt requires an initial set of samples to learn a preliminary model of the target function. This parameter is important if n_iter_relearn is 0 or too high.
- n_init_samples: Initial set of samples. Each sample requires a target function evaluation. [Default 10]
- init_method: (for continuous optimization only, unsigned integer) There are different strategies available for the initial design: [Default 1, LHS].
- Latin Hypercube Sampling (LHS)
- Sobol sequences
- Uniform Sampling
Random numbers are used frequently, from initial design, to MCMC, Thompson sampling, etc. They are based on the boost random number library.
- random_seed: If this value is positive (including 0), then it is used as a fixed seed for the boost random number generator. If the value is negative, a time based (variable) seed is used. For debugging or benchmarking purposes, it might be useful to freeze the random seed. [Default -1, variable seed].
Logging parameters
- verbose_level: (integer)
- Negative -> Error -> stdout
- 0 -> Warning -> stdout
- 1 -> Info -> stdout
- 2 -> Debug -> stdout
- 3 -> Warning -> log file
- 4 -> Info -> log file
- 5 -> Debug -> log file
- >5 -> Error -> log file
- log_filename: Name/path of the log file (if applicable, verbose_level>=3) [Default "bayesopt.log"]
Exploration/exploitation parameters
This is the set of parameters that drives the sampling procedure to explore more unexplored regions or improve the best current result.
- crit_name: Name of the sample selection criterion or a combination of them. It is used to select which points to evaluate for each iteration of the optimization process. Could be a combination of functions like "cHedge(cEI,cLCB,cPOI,cThompsonSampling)". See section Selection criteria for the different possibilities. [Default: "cEI"]
- crit_params, (n_crit_params): Array with the set of parameters for the selected criteria. If there are more than one criterion, the parameters are split among them according to the number of parameters required for each criterion. If the vector is empty or n_crit_params is 0, then the default parameters are selected for each criteria. [Default: crit_params = []]. For C, the array needs a size variable n_crit_params. In this case, default: n_crit_params = 0.
- epsilon: According to some authors [Bull2011], it is recommendable to include an epsilon-greedy strategy to achieve near optimal convergence rates. Epsilon is the probability of performing a random (blind) evaluation of the target function. Higher values implies forced exploration while lower values relies more on the exploration/exploitation policy of the criterion [Default 0.0 (epsilon-greedy disabled)]
- force-jump: Sometimes, specially when the number of initial points is too small, the learned model might be wrong and the optimization get stuck. Forced jumps measure the number of iterations where the difference between consecutive observations is smaller than the expected noise. Thus, we assume that any gain is pure noise and we could get more information somewhere else. This parameter sets the number of iterations with no gain before doing a random jump. If the parameter is 0, then this is disable. [Default 20]
Surrogate model parameters
The main advantage of Bayesian optimization over other optimization model is the use of a surrogate model. These parameters allow to configure it. See Section Surrogate models for a detailed description.
- surr_name: Name of the hierarchical surrogate function (nonparametric process and the hyperpriors on sigma and w). [Default "sGaussianProcess"]
- noise: Observation noise/signal ratio. [Default 1e-6]
- For stochastic functions (if several evaluations of the same point produce different results) it should match as close as possible the variance of the noise with respect to the variance of the signal. Too much noise results in slow convergence while not enough noise might result in not converging at all.
- For simulations and deterministic functions, it should be close to 0. However, to avoid numerical instability due to model inaccuracies, make it always greater than 0. For example, between 1e-10 and 1e-14.
- sigma_s: (only used for "sGaussianProcess" and "sGaussianProcessNormal") Known signal variance [Default 1.0]
- alpha, beta: (only used for "sStudentTProcessNIG") Inverse-Gamma prior hyperparameters (if applicable) [Default 1.0, 1.0]
Mean function parameters
This set of parameters represents the mean function (or trend) of the surrogate model.
- mean.name: Name of the mean function. Could be a combination of functions like "mSum(mConst, mLinear)". See Section Parametric (mean) functions for the different possibilities. [Default: "mConst"]
- mean.coef_mean, mean.coef_std: Mean function coefficients as vectors/array. [Default: "coef_mean=[1.0], coef_std=[1000.0]"]
- If the mean function is assumed to be known (like in "sGaussianProcess"), then coef_mean represents the actual values and coef_std is ignored.
- If the mean function has normal prior on the coeficients (like "sGaussianProcessNormal" or "sStudentTProcessNIG") then both the mean and std are used. The parameter mean.coef_std is a vector, it does not consider correlations.
- For C, the size of both arrays is defined in mean.n_coef.
Kernel parameters
The kernel of the surrogate model represents the correlation between points, which is related to the smoothness of the prediction.
- kernel.name: Name of the kernel function. Could be a combination of functions like "kSum(kSEARD,kMaternARD3)". See Section Kernel (covariance) models for the different posibilities. [Default: "kMaternARD5"]
- kernel.hp_mean, kernel.hp_std: Kernel hyperparameters normal prior in the log space. That is, if the hyperparameters are
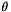, this prior is 
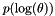. Any "ilegal" standard deviation (std<=0) results in a flat prior for the corresponding component. [Default:hp_mean=[1.0], hp_std=[10.0]]- If there are more than one kernel (a compound kernel), the parameters are split among them according to the number of parameters required for each criterion.
- ARD kernels require parameters for each dimension, if there are only one dimension provided (like in the default), it is copied for every dimension.
- For C, the size of both arrays is defined in kernel.n_hp.
Hyperparameter learning
Although BayesOpt tries to build a full analytic Bayesian model for the surrogate function, the kernel hyperparameters cannot be estimated in closed form. See Section Methods for learning the kernel parameters for a detailed description
- l_type: Learning method for the kernel hyperparameters. Currently, L_FIXED, L_EMPIRICAL and L_MCMC are implemented [Default L_EMPIRICAL]
- sc_type: Score function for the learning method. [Default SC_MAP]
- l_all: If true, all the parameters are learned (mean, sigma, etc.) using the method defined in l_type. If false, only the kernel hyperparameters are directly learned. [Default false]
Load/Save data parameters
We can select to store or restore data in files, to continue an optimization without starting over. The data is stored in plan text files. Thus, by modifying the files, this method can be used to preload existing datapoints in the model.
- load_save_flag: 1-Load data, 2-Save data, 3-Load and append data. Other values, no file saving or restore [Default 0]
- load_filename, save_filename; Filename to load/save data [Default "bayesopt.dat"]
